Phương pháp này dựa trên mối quan hệ giữa chuyên động tròn đều và dao động điều hòa. Nó thường được dùng để giải quyết các bài toán tìm thời gian, xác định thời điểm, xác định các đại lượng khác trong đó có giả thiết liên quan đến thời gian...

Tài liệu giới thiệu về phương pháp này rất nhiều, có trong các sách tham khảo, các tài liệu có trên mạng. Tuy nhiên, các tài liệu này chỉ mới xem xét và giới thiệu các bài toán ở mức độ cơ bản, sử dụng một vòng tròn để giải quyết các bài toán, chưa có nhiều bài khó được giới thiệu giải quyết bằng phương pháp này.
Do vậy, để hoàn thiện hơn nữa và giúp thí sinh thấy được đầy đủ phương pháp này, giáo viên sử dụng vòng tròn lượng giác trong một số bài toán lạ và khó. Cụ thể, sử dụng hai hay nhiều vòng tròn lượng giác lồng nhau (cùng tâm) để giải quyết bài toán liên quan đến dao động điều hòa có nhiều điều kiện, hoặc các bài toán hai hay nhiều dao động, bài toán tổng hợp dao động khó,…
Các bước giải chung là:
Bước 1: Vẽ hai hay nhiều vòng tròn lượng giác cùng tâm, khác bán kính.
Bước 2: Kẻ các trục gốc của các dao động điều hòa(căn cứ vào độ lệch pha và dấu các hàm điều hòa để vẽ).
Bước 3: Dựa vào giả thiết, thể hiện các thông tin trên các vòng tròn.
Bước 4: Sử dụng công cụ toán khác hỗ trợ giải quyết yêu cầu đề bài.
Dưới đây là chi tiết phương pháp này thông qua việc giới thiệu hai bài toán : Bài toán thỏa mãn nhiều điều kiện và bài toán xét quan hệ hai hay nhiều dao động.
Bài toán thỏa mãn nhiều điều kiện
Bài toán này có thể là các bài dao động cơ, sóng cơ, điện xoay chiều, dao động điện từ liên quan đến các đại lượng dao động điều hòa, nhưng giữa các đại lượng có mối quan hệ về pha, quan hệ về biên độ,…
Ví dụ: Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với chu kì 1,2 s. Trong một chu kì, nếu thời gian mà lực đàn hồi ngược chiều lực kéo về là 0,2 thì tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng:
A. 3
B. 4
C. 1
D. 2
Hướng dẫn giải: Trên hình vẽ, đường tròn lực kéo về có bán kính là k.A được thể hiện bằng đường liền, trục liền. Đường tròn lực đàn hồi là đường đứt có bán kính cũng là k.A (hai đường tròn trùng nhau nhưng gốc không trùng), tuy nhiên ta thể hiện hai đường tròn cho dễ phân biệt.
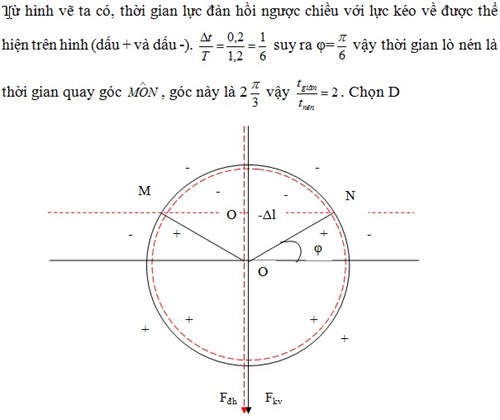
Bài toán xét quan hệ hai hay nhiều dao động
Nếu trong đề thi cho hai hay nhiều dao động điều hòa cùng phương cùng gốc tọa độ O, hoặc hai hay nhiều dao động thành phần của một dao động tổng hợp có cùng phương dao động thì phương pháp vòng tròn lượng giác cũng thường được áp dụng. Cụ thể tôi xin giới thiệu hai ví dụ mẫu và một số bài tập vận dụng sau
Ví dụ: Hai chất điểm dao động điều hoà với cùng tần số f = 0,25 Hz dọc theo hai đường thẳng song song cạnh nhau và song song với trục Ox. Vị trí cân bằng của hai chất điểm ở trên cùng một đường thẳng qua gốc toạ độ và vuông góc với trục Ox. Trong quá trình dao động, khoảng cách lớn nhất giữa hai chất điểm theo phương Ox là 16 cm. Tại thời điểm t, hai chất điểm đi ngang qua nhau. Thời gian ngắn nhất sau đó để khoảng cách giữa hai chất điểm bằng 8 cm theo phương Ox có giá trị là:
A. 1/12s
B. 1/4s
C. 1/3s
D. 1/6s
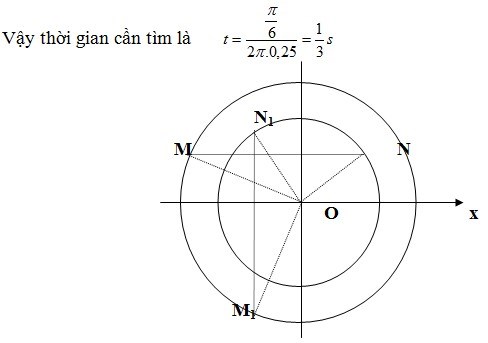
Hướng dẫn giải: Vẽ hai vòng tròn thể hiện cho hai dao động cùng tần số. biên độ A1=OM, A2=ON.
Giả sử chất điểm 1 dao động nhanh pha hơn chất điểm 2. Khi khoảng cách giữa hai chất điểm theo phương Ox là lớn nhất thì MN//Ox ta có MN=16cm.
Tại thời điểm t hai chất điểm đi ngang qua nhau (vị trí M1 và N1) ta có M1N1 vuông góc Ox.
Vị trí mà khoảng cách giữa hai chất điểm theo phương Ox bằng 8 là vị trí M2N2 có hình chiếu lên Ox bằng 8cm, mà M2N2=16cm. Vậy vị trí này M2N2 hợp với phương ngang góc 600 tức là hợp với M1N1 một góc 30 độ.
Nguồn Báo Giáo dục & Thời đại